Sign in Subscribe
논문리뷰

[GAN 시리즈][StyleGAN] A Style-Based Generator Architecture for Generative Adversarial Networks -1편

고재영

• 9 min read
[GAN 시리즈][StyleGAN] A Style-Based Generator Architecture for Generative Adversarial Networks -1편

1. Abstract

[제안한 네트워크]
Style transfer 문헌에서 차용한 Generative Adversarial Networks을 위한 alternative generator architecture을 제안한다.

[새로운 기능]
새로운 아키텍처는 자동으로 학습되고 비지도의 높은 수준의 속성(e.g., pose and identity when trained on human faces)과 생성된 이미지(e.g., 주근깨, 머리카락)의 stochastic variation을 separation하고 직관적으로 scale-specific control이 가능하게 한다.

새로운 generator는 traditional distribution quality metrics 측면에서 SOTA을 향상 시키고 더 나은 interpolation properties을 입증하며 latent factor of variation을 더 잘 disentangled 하게 한다.

interpolation quality와 disentanglement을 정량화(quantify) 하기 위해 모든 generator 아키텍처에 사용할 수 있는 두기자 새로운 자동화된 방법을 제안한다.

[새로운 데이터셋 제공]
마지막으로 매우 다양하고 고품질의 human faces 데이터셋을 소개한다.

2. PGGAN

PGGAN은 그림 1와 같이 점진적으로 낮은 해상도부터 높은 해상도까지 차근차근 점진적으로 생성하는 대표적인 생성 모델로써 StyleGAN의 base가 되는 모델로 latent vector \( z\)가 Normalize을 거쳐 모델에 바로 입력이 되는 형태로 학습이 진행됩니다. 이렇게 \( z\)가 Generator에 바로 입력으로 들어가면 GAN은 latent space가 무조건 학습 데이터셋의 확률분포와 비슷한 형태로 만들어 지도록 학습을 하게 됩니다. 이렇게 되면 latent space가 entangle하게 만들어 지게 됩니다.

StyleGAN을 이해하려면 entangle와 disentangle의 차이를 알아야 하기 때문에 간단하게 비교를 해보도록 하겠습니다.

  • entangle
    • 서로 얽혀 있는 상태여서 특징 구분이 어려운 상태. 즉, 각 특징들이 서로 얽혀있어서 구분이 안됨
  • disentangle
    • 각 style들이 잘 구분 되어있는 상태여서 어느 방향으로 가면 A라는 특징이 변하고 B라는 특징이 변하게 되어서 특징들이 잘 분리가 되어있다는 의미.
    • 선형적으로 변수를 변경했을 때 어떤 결과물의 feature인지 예측할 수 있는 상태.
(그림 1) PGGAN Architecture

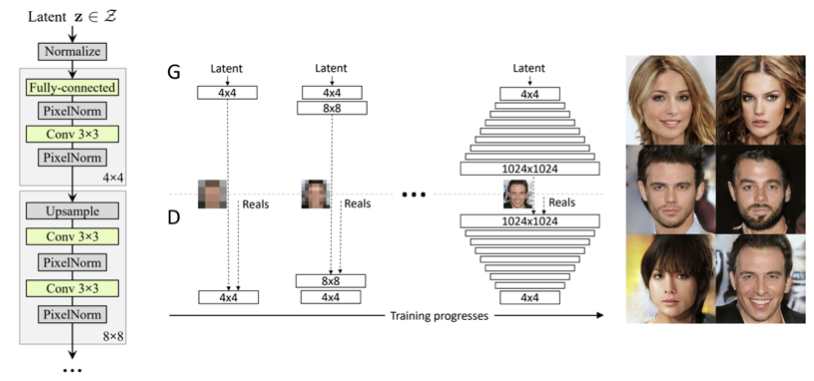
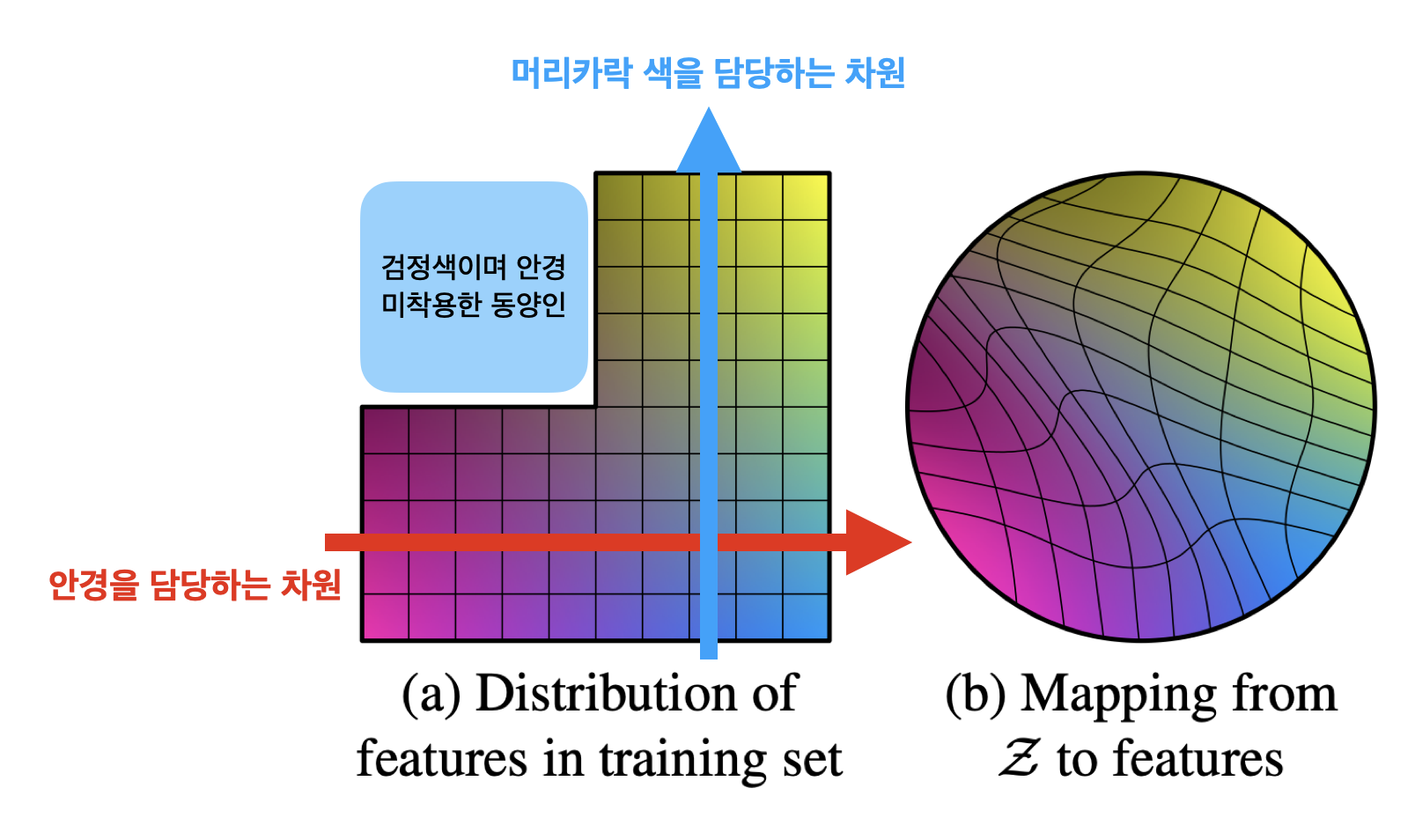
그림 2(a)는 학습 데이터셋을 시각적으로 보여주는 그림입니다. 더 나은 이해를 돕고자 예시를 들어 설명을 해보면, 학습 데이터셋에는 검정 머리이며 안경을 착용한 동얀인으로 구성되었다고 가정 합니다. 붉은색 화살표는 안경을 담당하는 차원이고 파란색 화살표는 머리카락 색을 담당하는 차원 입니다. PGGAN처럼 latent variable을 기반으로 학습하는 생성 모델은 noise 상태에 있는 latent space \( \mathcal{Z}\)을 학습 데이터 분포와 비슷하게 변화시키는 mapping을 학습하는 것을 목표로 합니다. 만약 학습 데이터셋에 없는 데이터 분포인 머리카락 색이 검정색이며 안경을 미착용한 동양인을 생성하고 싶어도 학습 데이터의 고정된 분포를 latent space가 non-linear하게 mapping이 되어버린 상태여서 생성하기 매우 어렵습니다.

(그림 2)

2-1. PGGAN으로 이미지 생성하기

GAN이 잘 학습이 된 상태라면 이제 생성 모델을 이용해서 이미지를 생성할 경우 latent variable 기반의 생성 모델은 가우시안 분포 형태의 random noise을 입력으로 넣어주게 됩니다. 학습 데이터셋의 특징에 mapping 되어있는있는 latent space \( \mathcal{Z}\)는 n차원의 가우시안 분포로 구성되어서 그림 2(b)와 같은 형태입니다. (a)의 텅 비어있는 부분이 있는 상태에서 mapping을 시켜주니까 억지로 끼어맞추기 하는 형식으로 mapping이 이루어지다보니 wrapping이 발생하게 됩니다.

wrapping이 발생하게 되면 생성된 이미지의 머리카락 색깔이 갑자기 다른 형태와 색으로 급진적으로 변화되어 어떤 생성 이미지가 나올지 예측할 수 없을 정도로 급진적으로 변하게 되는 특징이 존재합니다.

3. StyleGAN

StyleGAN의 아이디어는 마치 화가가 눈동자 색만 다른 색으로 색칠하고, 머리카락 색만 다른 색으로 색칠하고 하는 것 처럼 PGGAN에서도 style들을 변형시키고 싶은데 Generator에 latent vector \( z\)가 바로 입력되게 때문에 entangle하게 되어서 불가능 하다는 단점이 있었습니다. 그래서 논문 저자는 style transfer처럼 원하는 style로 수치화 시켜서 GAN에 적용 하고자 하였습니다. 그래서 나온 아이디어가 각각 다른 style을 여러 scale에 넣어서 학습 시키는 방법입니다.

하지만 latent variable 기반의 생성 모델은 가우안 분포 형태의 random noise을 입력으로 넣어주는 특징을 갖고 있어 latent space가 entangled하게 됩니다. 따라서 StyleGAN은 학습 데이터셋이 어떤 분포를 갖고 있을지 모르니 GAN에 \( z\)을 바로 넣어주지 말고 학습 데이터셋과 비슷한 확률 분포를 갖도록 non-linear하게 mapping을 우선적으로 하고 mapping된 \( z\)을 이용하면 좀 더 학습하기에 쉽지 않을까? 하는 아이디어로 그림 3처럼 Mapping Network을 사용해 mapping된 \( \mathcal{W}\)을 각 scale에 입력으로 넣어서 학습을 시키게 됩니다.

(그림 3) StyleGAN Architecture

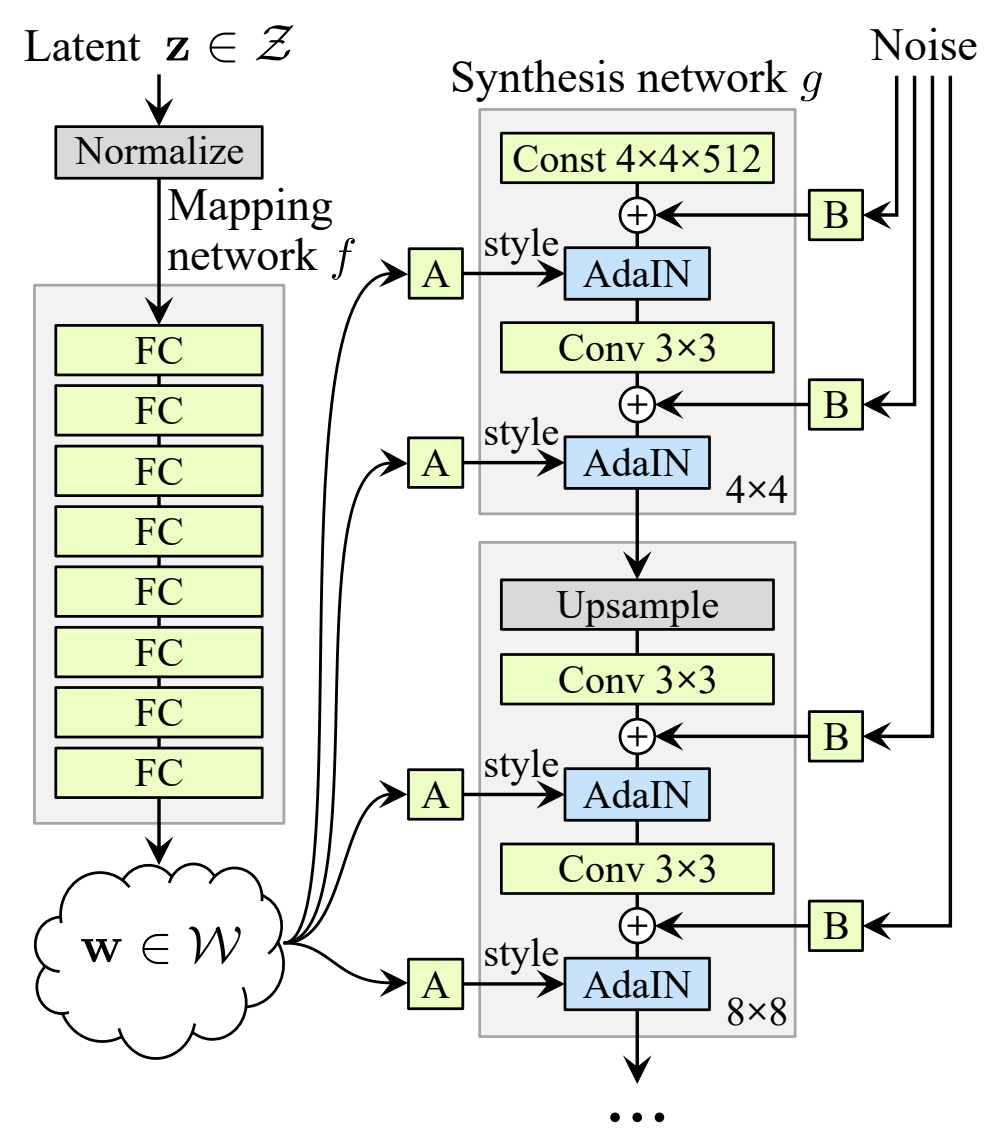
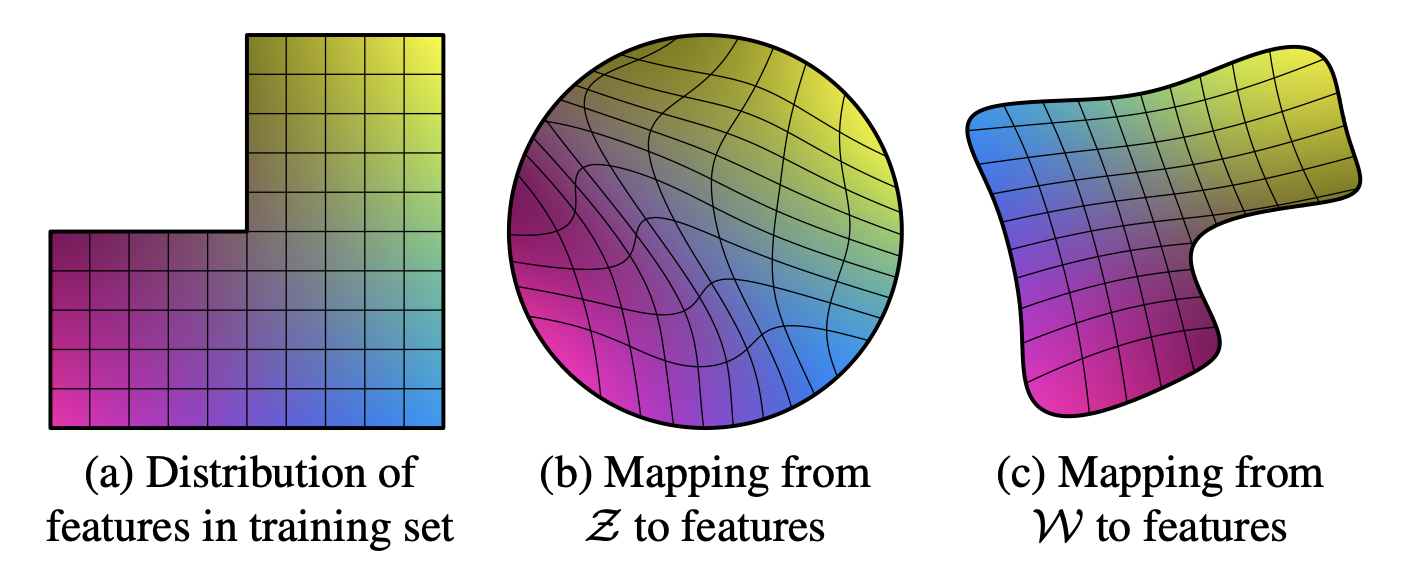
Mapping Network를 통해서 나온 \( \mathcal{W}\)는 정확하지는 않지만 학습 데이터셋의 확률 분포와 비슷한 모양으로 우선 mapping이 된 상태이기 때문에 그림 4(c)처럼 특징이 mapping된 latent space의 \( \mathcal{W}\)가 disentangle하게 됩니다.

(그림 4)

AdaIN

AdaIN의 기능을 설명하기에 앞서 기본적인 예로 Neural Network을 한번 살펴봅시다. Neural Network에서 각 layer를 지나가며 scale, variance의 변화가 생기는 일이 빈번하게 발생하며 이는 학습이 불안정 해지는 현상을 발생합니다. 따라서 이를 방지하기 위해 Batch Normalization 방법같은 normalization 기법을 각 layer에 사용하므로써 해결하곤 합니다.

StyleGAN에서는 Mapping network를 거쳐서 나온 \( \mathcal{W}\)가 latent vector의 style로 각 scale을 담당하는 layer에 입력으로 들어가게 됩니다. 위에서도 언급하다 싶이 Neural Network에서 layer를 지나가면 scale, variance의 변화가 발생하여 학습이 불안정하게 됩니다. 이때 해결하는 방법이 normalization 기법을 사용한다고 언급을 했습니다. 따라서 본 논문에서는 \( \mathcal{W}\)가 style에 영향을 주면서 동시에 normalization 해주는 방법으로 사용하게 됩니다. AdaIN의 수식은 다음과 같습니다.

$$ AdaIN(x_i, y) = y_{s, i} \cfrac{x_i - \mu(x_i)}{\sigma(x_i)} + y_{b, i} $$

  • \( y_{s, i}\)라는 linear cofficient를 곱해주고 상수를 더합니다.
  • \( y_{s, i}\)와 \( y_{b, i}\)는 \( \mathcal{W}\)를 Affine Transformation을 거쳐서 shape을 맞추고 style을 입혀주게 됩니다.

수식을 보면 표준편차로 나누고 평균으로 뺀 값이니까 random variable을 정규화 시키는 것 입니다. 즉, instance에 대해 normalization 해주는 것 이라고 볼 수 있습니다.

간단하게 정리를 해보자면

  • \( \mathcal{W}\)가 AdaIN을 통해 style을 입힐 때 shape이 안맞아 Affine Transformation을 거쳐서 shape을 맞춰줍니다.
  • layer를 거치면 학습이 불안정해져서 normalization을 각 layer에다 추가하는데 StyleGAN에서는 그 역할을 AdaIN이 합니다.
  • style을 입히는 개념은 \( y_{s, i}\)곱하고 \( y_{b, i}\)를 더하는 과정입니다.
  • AdaIN에서 정규화를 할 때 마다 한번에 하나씩만 \( \mathcal{W}\)가 기여하므로 하나의 style이 각각의 scale에서만 영향을 끼칠 수있도록 분리를 해주는 효과를 갖습니다. 따라서 본 논문 저자들은 style을 분리하는 방법으로 AdaIN이 효과적이라고 말을 하고 있습니다.

Sign up for more like this.

Enter your email
Subscribe